Slovenski Saab portal - Malo mehanike kotalnega trenja

Malo mehanike kotalnega trenja

Blaž Bat a.k.a. Piston

sobota, 28 april 2007

Fantje iz portala so me spodbudili da spišem članek na temo kotalnega trenja oz. mehanike oprijema pnevmatike s cestiščem. Sicer nima direktne veze z SAABi, vendar je zanimiva, ter mislim da tudi uporabna.

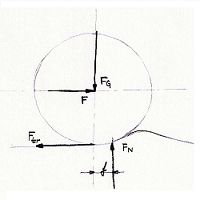
Začel bom kar v srednji oziroma osnovni šoli.Srednješolska fizika uči da je sila trenje produkt sile s katero telo deluje na podlago ter koeficienta trenja med podlago ter opazovanim telesom. Kar se kotalnega trenja tiče pa je povedano samo to (če sploh), da se med kotaljenjem zaradi deformacije telesa in tal prijemališče sile podlage premakne naprej za razdaljo f, ter tako ustvari moment ki nasprotuje gibanju.

V tem članku bom skušal nadgraditi razumevanje tega pojava. Razložiti bom poizkušal kaj nam kot voznikom to pomeni, ter zakaj do tega pride.

Fizikalni model

če želimo nek zapletenejši fizikalni proces opisati, ter ovrednotiti se poslužujemo fizikalnih modelov. Kompleksne probleme rešujemo tako, da med seboj interaktivno povežemo več osnovnih fizikalnih modelov, pri katerih znamo dogajanje zadosti natančno popisati. Na ta način nadomestimo zapleten proces, na več (osnovnih) procesov, ki omogočajo enostavnejšo analizo dogajanja.

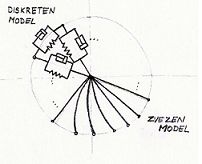
Avtomobilsko pnevmatiko si lahko (z malo domišlije) predstavljamo kot ščetine (podobno kot krtače v avtopralnici), ki so med seboj povezane z vzmetni in dušilkami. Tak fizikalni model je uporaben tudi za trše materiale (naprimer kroglice v ležajih)

če ta model še nekoliko zakompliciramo in togost in dušenje vsaki ščetini zvezno porazdelimo po dolžini, dobimo model, na katerem je deformacija pnevmatike lepo vidna

Zdrs (slip) pnevmatike

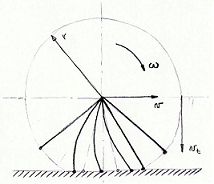
Jasno je da pnevmatika na avtomobilu pretvarja rotirajoče gibanje v ravninsko (translatorno) gibanje, pri tem pa kot pri vsakem realnem procesu spreminjanja energijske bilance nastanejo izgube. Pri tornih gonilih (kar pnevmatika je) se nam te izgube kažejo kot slip oz. zdrs pnevmatike napram tlom.

Slip bi lahko definirali kot dejansko obodno hitrost kolesa ( ) napram realni hitrosti s katero se kolo giblje npr. težišče tega kolesa. če to razmerje delimo z obodno hitrostjo ter množimo z 100% dobimo relativni zdrs ali slip.

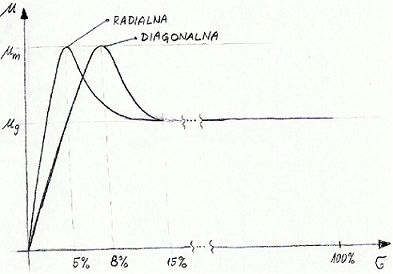
Sedaj lahko narišemo diagram koeficienta trenja v odvisnosti od relativnega slipa dobimo karakteristiko pnevmatike, ki nam pove, koliko deformacije je pnevmatika sposobna absorbirati preden zdrsne. (Ko je slip enak 0 se kolo vrti brez vsakršnega drsenja, ko pa je 100 se kolo vrti v prazno, na mestu.)

V diagramu je narisana primerjava med radialno ter diagonalno pnevmatiko. Vidimo da je diagonalna pnevmatika sposobna absorbcije večjih deformacij preden zdrsne. Podobna zgodba je v primerjavi zimska-letna guma.

Graf je narisan do približno 15%, saj je v tem območju vse pomembno dogajanje.

Iz diagrama je vidno, da sposobnost prenašanja sile z večanjem slipa narašča, dokler ne dosežemo maksimalne vrednosti. Tedaj kolo zdrsne, ter sposobnost prenašanja sile postane odvisna od trenja pri drsenju, ter se z večanjem slipa ne spreminja več.

Dejansko dogajanje je najlažje razumeti tako, da si predstavljamo pospeševanje avtomobila na ravni cesti. Recimo, da je maksimalna deformacija radialne pnevmatike 5%, diagonalne pa 8% (številke so izmišljene), ter da je moment (navor) avtomobila na kolesu zadosten da v pnevmatiko vnesemo največ 4% deformacije. To pomeni, da bi na podlagi brez ovir z obema pnevmatikama pospeševali enako hitro, tj. brez da bi se kolesi vrteli v prazno.

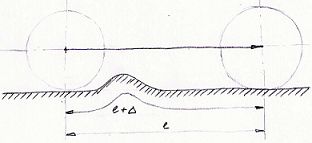
če pa na podlago dodamo grbino, ki bi v pnevmatiko vnesla še recimo 3% deformacije (ko gre pnevmatika čez grbino mora opraviti daljšo pot, zato se mora dodatno deformirati), bi to pomenilo da bi radialna pnevmatika zdrsnila (ker bi bila skupna deformacija večja kot jo guma dopušča), ter se začela vrteti v prazno (v diagramu bi šla ??�čez??� vrh največjega trenja), diagonalna pa bi nadaljevala s pospeševanjem, brez vrtenja v prazno.

Na tem mestu bi dodal še zanimivost o trenju, ki jo občutimo pri prehitri vožnji skozi ovinek.

Ko enkrat premagamo silo trenja (lepenja) v eni smeri, je sila trenja (lepenja) premagana v vseh smereh.
Tukaj se lahko naredi preprost preizkus. Na neko strmino položimo nek predmet, ki dokler ga ne tikamo, na strmini miruje. Ta predmet nato začnemo potiskati v smeri vzporedno na strmino (vodoravna smer). Kaj se zgodi? Naš predmet začne drseti po klancu navzdol, čeprav ga v tej smeri ne potiskamo in je prej miroval.
Ta pojav je razlog za pravilo v vožnji skozi ovinke, ki pravi da je treba ovinke voziti brez ??�gasa??�.

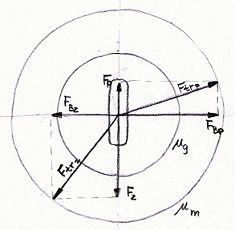
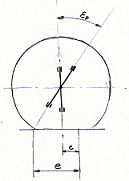
Na gornji sliki je narisano kako zaviranje (indeks z) ali pospeševanje (indeks p) znižuje sposobnost oprijema gume na bočne sile, ki so posledica zavijanja.

Na sliki predstavlja večji krog silo/koeficient trenja pri mirovanju (guma še ne drsi), manjši krog pa silo/koeficient trenja pri gibanju. Ko presežemo silo trenja pri mirovanju začne kolo drseti. če hočemo, da nazaj dosežemo oprijem brez drsenja moramo silo na kolo zmanjšati pod mejo trenja pri drsenju (ne pa pod mejo trenja pri mirovanju). To storimo tako, da zmanjšamo tangencialno silo na kolo (nehamo zavirati oz. pospeševati) ali pa zmanjšamo zasuk volana in tako zmanjšamo aksialno silo na kolo. Ko se kolo spet vrti brez drsenja lahko silo na kolo ponovno povečamo do meje trenja pri mirovanju.

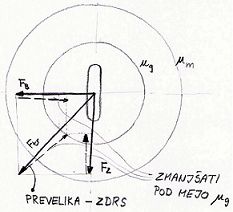
Iz tega lahko zaključimo, da lahko v ovinek najhitreje zapeljemo, če na kolo ne deluje nobena tangencialna sila (ni nobene sile, ki bi zavirala ali pospeševala). To hkrati pomeni da tisto pravilo ??�brez gasa??� ni najbolj natančno, saj v tem primeru kolesa še vedno nekoliko zavira motor, in s tem manjša potencial oprijema na bočne sile. Idealno bi bilo, da bi pogonskim kolesom dodajali ravno toliko momenta kot je moment ki nasprotuje vrtenju koles (to je tisti moment, ki nastane zaradi koeficinte kotalnega trenja f), vendar je to skoraj nemogoče doseči, še posebej, ko nam že teče voda v grlo. Takrat se najbolj enostavno približamo temu ??�idealu??� tako, da stisnemo sklopko.

Koeficient kotalnega trenja V začetku sem omenjal, da je koeficient kotalnega tenja posledica premika prijemališča sile podlage za razdaljo f. Zakaj se prijemališče sile premakne bom pa skušal razložiti sedaj.

Za razlago je ponovno najbolj primeren model iz začetka tega sestavka.

če gumo položimo na podlago ter jo obremenimo z silo, ki deluje navpično navzdol (teža recimo), brez da bi jo vrteli ali kamorkoli potiskali dobimo naslednjo razporeditev napetosti v gumi:

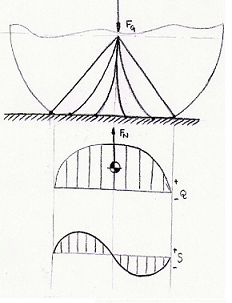
Kjer je Q deformacija zaradi obtežbe (npr. teža avtomobila), S pa deformacija pnevmatike v vodoravni smeri. Rečemo lahko tudi, da predstavlja Q mejo trenja (pri mirovanju ali gibanju), S pa je neka lastnost pnevmatike.
če bi za ta primer računali težišče lika pod krivuljo Q, bi to ležalo točno na sredini dotikalne površine pnevmatike z podlago, oziroma točno pod vrtiščno osjo kolesa, kar pomeni, da bi bil koeficient kotalnega trenja f enak 0.
Sedaj začnemo kolo porivati v vodoravni smeri tako, da začne nakotaljevati. Stanje je sledeče:

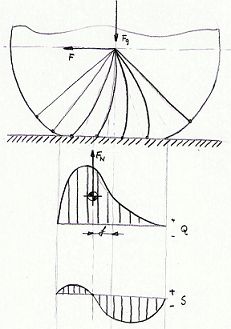
Vrh krivulje Q se premakne v smeri potiskanja kolesa, S pa se premakne v nasprotni smeri. V tem primeru bi bilo težišče lika pod krivuljo Q zamaknjeno v stran od srednjice kolesa natanko za vrednost kotalnega trenja f. (Vrednost f je odvisna od hitrosti.)

če sedaj preSlikamo krivuljo Q prek x osi (narišem mejo pri mirovanju in gibanju), ter jo položimo čez krivuljo S, lahko grafično določimo kolikšen del pnevmatike v oprijemu dejansko na podlagi miruje in kolikšen po podlagi drsi.

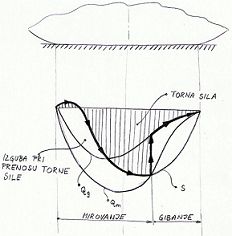
Do kje pnevmatika miruje določimo tako, da potujemo po krivulji S do presečišča z krivuljo Q pri mirovanju. Na tem mestu elastična lastnost pnevmatike prekorači njeno mejo trenja (pri mirovanju). Od te točke naprej pnevmatika drsi, to pomeni, da pademo na tem mestu na mejo trenja pri drsenju (glej puščice na sliki) (če kolo že prej zablokira se ves čas gibljemo po krivulji Q za trenje pri gibanju). Velikost površine pod tem novim, skombiniranim diagramom pa predstavlja skupno torno silo, ki jo je pnevmatika sposobna prenesti.

To si lahko predstavljamo tako, da do določene točke guma sprejema deformacijo, v naslednjem trenutku pa te deformacije ne more več absorbirati ter zdrsne. Od tu potem dobimo slip tornega gonila.

če sedaj predpostavimo še, da vozimo po cestišču kjer ostaja voda, se poleg znižanega koeficienta trenja zgodi še to, da nam prednji del pnevmatike (tisti ki ponavadi miruje, glej gornjo sliko) odriva vodo izpod gume, in zato ne leži še na podlagi. Pod tistim delom pnevmatike torej nimamo ne trenja pri mirovanju, ne trenja pri drsenju, temveč tekočinsko trenje, katero je sposobno prenašati še manjše sile kot trenje pri drsenju. čas oz. delež gume, ki izpodriva vodo je seveda odvisen od hitrosti. Pri zelo majhnih hitrostih se nahaja blizu nič, z večanjem hitrosti pa narašča dokler celotna pnevmatika ne izgubi stika z podlago. Takrat pride do znanega pojava, aquaplaninga.

Podobno velja za bočne oz. aksialne sile na kolo.

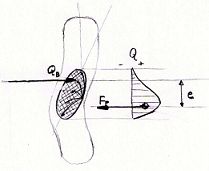
Tudi tukaj se razporeditev sile spremeni med gibanjem, in tako kot pri prejšnjem primeru dobimo neko zamaknitev e prijemališča sile napram vrtišču kolesa. Ta zamaknitev kolesa nam da t.i. stabilizacijski hitrostni moment ( ), kateri je odgovoren za to, da se nam kolesa, ko volan izpustimo poravnajo v smer vožnje. Od te razdalje e, je tudi odvisen naš občutek dogajanja pod kolesi (informacije iz cestišča).
Ta razdalja se spreminja v odvisnosti kota zasuka volana ter hitrosti, in bi bila, pri večjih hitrostih celo negativna. To bi pa pomenilo da nebi mogli niti za trenutek izpustiti volana iz rok, saj bi se kolesa obrnila pravokotno na smer vožnje. Ta problem je rešen tako, da je prema koles nagnjena za določen kot nazaj, ter je razdalja e na ta način umetno povečana, s tem pridobimo na stabilnosti in občutku dogajanja pod kolesi.

To bi tudi bilo iz stališča mehanike na hitro nekako vse. Dodal bi še edino to, da je pri vsej tej razlagi upoštevano, da guma nalega na gladko površino. S tem sem izključil faktor spreminjajoče se podlage. To fizikalno pomeni, da nisem upošteval dodatnega faktorja, ki bi povečeval torno silo. Poenostavitev sem uporabil, ker je do neke mere že upoštevana pri koeficientih trenja, pa tudi zaradi dejstva, da na opisane pojave vpliva celotna konstrukcija pnevmatike, na oblikovni oprijem pa v večji meri samo guma na pnevmatiki.

Upam da je bilo branje zanimivo ter predvsem razumljivo. če karkoli ni jasno pa vprašajte, bom poizkusil razložiti.

Napiši komentar

Komentarje lahko pišejo samo registrirani uporabniki.
Prijavite se!